1、哈密尔顿算子: $\nabla$ -nabla
在介绍梯度等概念之前,首先引入CFD非常常见的运算符之一: $\nabla$, 它是某一物理量在三个坐标方向的偏导数的矢量和, 定义如下:
\[\nabla=\frac{\partial}{\partial x} \mathbf{i}+\frac{\partial}{\partial y} \mathbf{j}+\frac{\partial}{\partial z} \mathbf{k}\]2、梯度(Gradient)
当 $\nabla$ 作用于标量 $s$ 时即可得到该标量在空间中的梯度,下面列出了CFD中梯度的各种表达形式:
\[\operatorname{grad} s=\nabla \cdot s=\nabla s=\frac{\partial s}{\partial x_ {i}}=\frac{\partial s}{\partial x} \mathbf{i}+\frac{\partial s}{\partial y} \mathbf{j}+\frac{\partial s}{\partial z} \mathbf{k}\]可以看出标量场的梯度是一个矢量场,它表示 $s$ 在空间某一位置沿某一方向的变化量。如果想要的到 $s$ 在某一特定方向 $\mathbf{e}_ {l}$ (方向 $l$ 上的单位矢量 $)$ 上的梯度,即方向导数,则可以根据矢量点乘的几何意义来进行计算:
\[\frac{d s}{d l}=\nabla s \cdot \mathbf{e}_ {l}=\|\nabla s\| \cos \left(\nabla s, \mathbf{e}_ {l}\right)\]由此可见,当 $\cos \left(\nabla s, \mathbf{e}_ {l}\right)=1$ , 即空间任意方向 $l$ 与梯度方向一致时沿该方向具有最大梯度,因此 $\nabla s$ 代表了空间中任意点上梯度变化最大的方向和变化量,而且 $\nabla s$ 垂直于该点处的等值线或等值面。
3、散度 (Divergence)
根据矢量点乘的运算规则, $\nabla$ 与一个矢量的点乘是一个标量,它代表了矢量场的散度:
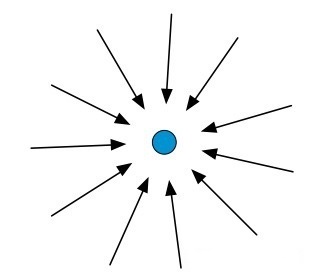
\[\operatorname{div} \mathbf{v}=\nabla \cdot \mathbf{v}=\frac{\partial u_ {i}}{\partial x_ {i}}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\]可以看出矢量的散度是一个标量,在CFD中它表示空间中某一区域流入或流出的矢量的多少,比较典型的例子有点源或者点汇。如下图是一个点汇,周围的矢量均流向该点。
标量的梯度为矢量,因此对该矢量可以继续求散度,从而引入拉普拉斯算子 $\Delta=\nabla \cdot \nabla=\nabla^{2}$ :
\[\nabla \cdot(\nabla s)=\nabla^{2} s=\frac{\partial^{2} s}{\partial x_ {i}^{2}}=\frac{\partial^{2} s}{\partial x^{2}}+\frac{\partial^{2} s}{\partial y^{2}}+\frac{\partial^{2} s}{\partial z^{2}}\]上式代表了梯度的散度,可以看出标量经过拉普拉斯算子运算以后仍然是标量。 矢量的散度为标量,因此对该标量可以继续求梯度:
\[\nabla \cdot(\nabla \cdot \mathbf{v})=\nabla^{2} \mathbf{v}=\nabla^{2} u_ {i}=\left(\nabla^{2} u\right) \mathbf{i}+\left(\nabla^{2} v\right) \mathbf{j}+\left(\nabla^{2} w\right) \mathbf{k}\]4、旋度(curl)
旋度是由 $\nabla$ 与矢量的叉乘得到,它的运算结果是一个矢量,代表了矢量做旋转运动的方向和强度:
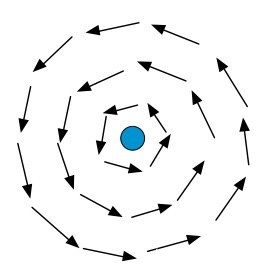
\[\nabla \times \mathbf{v}=\left(\frac{\partial}{\partial x} \mathbf{i}+\frac{\partial}{\partial y} \mathbf{j}+\frac{\partial}{\partial z} \mathbf{k}\right) \times(u \mathbf{i}+v \mathbf{j}+w \mathbf{k})= \left \vert\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ u & v & w\end{array}\right \vert\] \[=\left(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\right) \mathbf{i}+\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right) \mathbf{j}+\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) \mathbf{k}\]一个典型的有旋流场是点涡,如下图所示,它展示了一个散度为0的有旋矢量场。