1、主要函数
函数 distmesh2d( )
DISTMESH2D 2-D Mesh Generator using Distance Functions.
[P,T]=DISTMESH2D(FD,FH,H0,BBOX,PFIX,FPARAMS)
% P: Node positions (Nx2), 网格点的x,y坐标
% T: Triangle indices (NTx3), 三角形单元的三个顶点索引
% FD: Distance function d(x,y), 给定任一点到边界的距离函数
% FH: Scaled edge length function h(x,y), 网格大小的函数
% H0: Initial edge length, 网格的大小
% BBOX: Bounding box [xmin,ymin; xmax,ymax], 最大外围矩形范围
% PFIX: Fixed node positions (NFIXx2), 网格中需要固定的点坐标,也就是一定需要出现在网格中的点
% FPARAMS: Additional parameters passed to FD and FH
dptol=.001; ttol=.1; Fscale=1.2; deltat=.2; geps=.001*h0; deps=sqrt(eps)*h0;
densityctrlfreq=30;
% 1. Create initial distribution in bounding box (equilateral triangles)
[x,y]=meshgrid(bbox(1,1):h0:bbox(2,1),bbox(1,2):h0*sqrt(3)/2:bbox(2,2));
x(2:2:end,:)=x(2:2:end,:)+h0/2; % Shift even rows
p=[x(:),y(:)]; % List of node coordinates
% 2. Remove points outside the region, apply the rejection method
p=p(feval(fd,p,varargin{:})<geps,:); % Keep only d<0 points
r0=1./feval(fh,p,varargin{:}).^2; % Probability to keep point
p=p(rand(size(p,1),1)<r0./max(r0),:); % Rejection method
if ~isempty(pfix), p=setdiff(p,pfix,'rows'); end % Remove duplicated nodes
pfix=unique(pfix,'rows'); nfix=size(pfix,1);
p=[pfix; p]; % Prepend fix points
N=size(p,1); % Number of points N
count=0;
pold=inf; % For first iteration
clf,view(2),axis equal,axis off
while 1
count=count+1;
% 3. Retriangulation by the Delaunay algorithm
if max(sqrt(sum((p-pold).^2,2))/h0)>ttol % Any large movement?
pold=p; % Save current positions
t=delaunayn(p); % List of triangles
pmid=(p(t(:,1),:)+p(t(:,2),:)+p(t(:,3),:))/3; % Compute centroids
t=t(feval(fd,pmid,varargin{:})<-geps,:); % Keep interior triangles
% 4. Describe each bar by a unique pair of nodes
bars=[t(:,[1,2]);t(:,[1,3]);t(:,[2,3])]; % Interior bars duplicated
bars=unique(sort(bars,2),'rows'); % Bars as node pairs
% 5. Graphical output of the current mesh
cla,patch('vertices',p,'faces',t,'edgecol','k','facecol',[.8,.9,1]);
drawnow
end
% 6. Move mesh points based on bar lengths L and forces F
barvec=p(bars(:,1),:)-p(bars(:,2),:); % List of bar vectors
L=sqrt(sum(barvec.^2,2)); % L = Bar lengths
hbars=feval(fh,(p(bars(:,1),:)+p(bars(:,2),:))/2,varargin{:});
L0=hbars*Fscale*sqrt(sum(L.^2)/sum(hbars.^2)); % L0 = Desired lengths
% Density control - remove points that are too close
if mod(count,densityctrlfreq)==0 & any(L0>2*L)
p(setdiff(reshape(bars(L0>2*L,:),[],1),1:nfix),:)=[];
N=size(p,1); pold=inf;
continue;
end
F=max(L0-L,0); % Bar forces (scalars)
Fvec=F./L*[1,1].*barvec; % Bar forces (x,y components)
Ftot=full(sparse(bars(:,[1,1,2,2]),ones(size(F))*[1,2,1,2],[Fvec,-Fvec],N,2));
Ftot(1:size(pfix,1),:)=0; % Force = 0 at fixed points
p=p+deltat*Ftot; % Update node positions
% 7. Bring outside points back to the boundary
d=feval(fd,p,varargin{:}); ix=d>0; % Find points outside (d>0)
dgradx=(feval(fd,[p(ix,1)+deps,p(ix,2)],varargin{:})-d(ix))/deps; % Numerical
dgrady=(feval(fd,[p(ix,1),p(ix,2)+deps],varargin{:})-d(ix))/deps; % gradient
dgrad2=dgradx.^2+dgrady.^2;
p(ix,:)=p(ix,:)-[d(ix).*dgradx./dgrad2,d(ix).*dgrady./dgrad2]; % Project
% 8. Termination criterion: All interior nodes move less than dptol (scaled)
if max(sqrt(sum(deltat*Ftot(d<-geps,:).^2,2))/h0)<dptol, break; end
end
% Clean up and plot final mesh
[p,t]=fixmesh(p,t);
simpplot(p,t)
2、例子
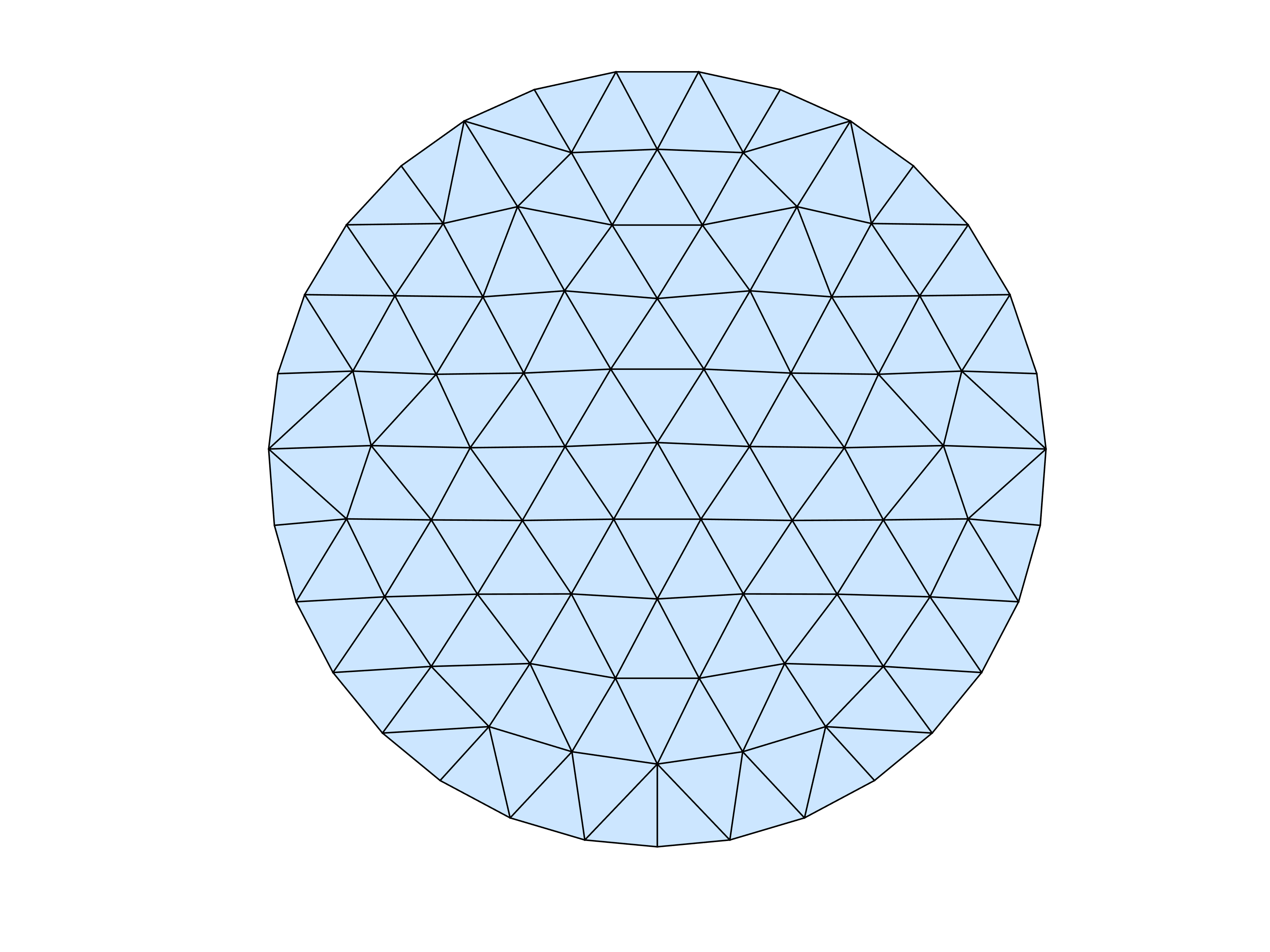
Example: (Uniform Mesh on Unit Circle)
fd=@(p) sqrt(sum(p.^2,2))-1;
[p,t]=distmesh2d(fd,@huniform,0.2,[-1,-1;1,1],[]);
Example: (Rectangle with circular hole, refined at circle boundary)
fd=@(p) ddiff(drectangle(p,-1,1,-1,1),dcircle(p,0,0,0.5));
fh=@(p) 0.05+0.3*dcircle(p,0,0,0.5);
[p,t]=distmesh2d(fd,fh,0.05,[-1,-1;1,1],[-1,-1;-1,1;1,-1;1,1]);

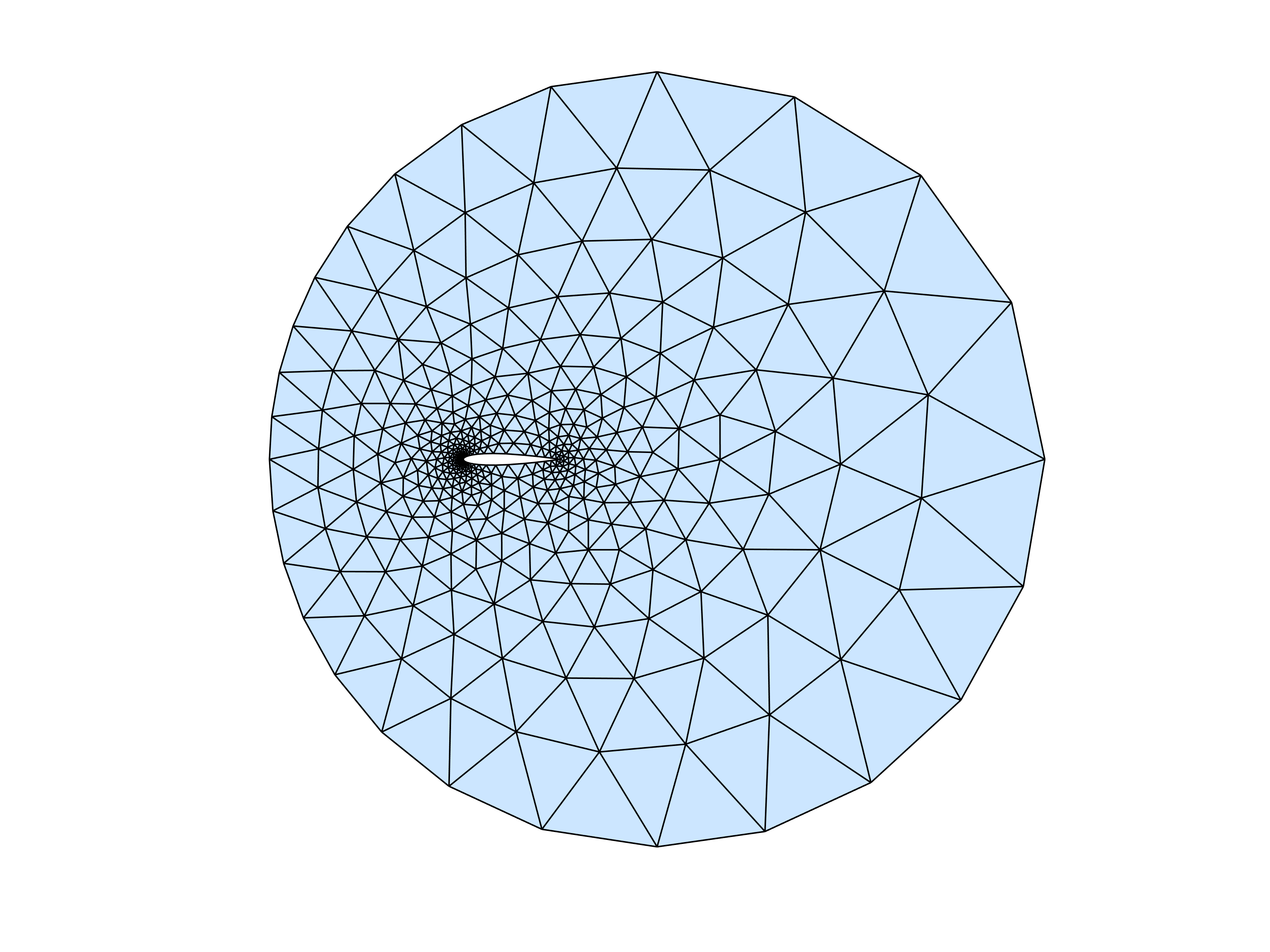
Example: (NACA0012 airfoil)
hlead=0.01; htrail=0.04; hmax=2; circx=2; circr=4;
a=.12/.2*[0.2969,-0.1260,-0.3516,0.2843,-0.1036];
fd=@(p) ddiff(dcircle(p,circx,0,circr),(abs(p(:,2))-polyval([a(5:-1:2),0],p(:,1))).^2-a(1)^2*p(:,1));
fh=@(p) min(min(hlead+0.3*dcircle(p,0,0,0),htrail+0.3*dcircle(p,1,0,0)),hmax);
fixx=1-htrail*cumsum(1.3.^(0:4)');
fixy=a(1)*sqrt(fixx)+polyval([a(5:-1:2),0],fixx);
fix=[[circx+[-1,1,0,0]*circr; 0,0,circr*[-1,1]]'; 0,0; 1,0; fixx,fixy; fixx,-fixy];
box=[circx-circr,-circr; circx+circr,circr];
h0=min([hlead,htrail,hmax]);
[p,t]=distmesh2d(fd,fh,h0,box,fix);