1. 原理简介
一维Maxwell方程组形式如下
\[\left\{ \begin{aligned} \varepsilon(x) \frac{\partial E}{\partial t}=-\frac{\partial H}{\partial x}\\ \mu(x) \frac{\partial H}{\partial t}=-\frac{\partial E}{\partial x} \end{aligned} \right. \label{eq1} \tag{1}\]其中 $(E,H)$ 分别表示电场强度和磁场强度,材料参数 $\varepsilon{(x)}$ 与 $\mu{(x)}$ 分别表示介电常数和磁导率。
设边界条件为 $x\in [-1,1]$ 且 $E(-1,t) = E(1,t) =0$,$\varepsilon{(x)}$ 和 $\mu{(x)}$ 在 $x=0$ 处不连续,材料参数为分片常数。为构造离散格式,采用常规方法并寻求近似解 $(E,H)\simeq (E_{h},H_{h})$ 为 $K$ 个局部多项式 $(E_{h}^{k}, H_{h}^{k})$ 的直和
\[\left[\begin{array}{c} E_{h}^{k}(x, t) \\ H_{h}^{k}(x, t) \end{array}\right]=\sum_{i=1}^{N_{p}}\left[\begin{array}{c} E_{h}^{k}\left(x_{i}^{k}, t\right) \\ H_{h}^{k}\left(x_{i}^{k}, t\right) \end{array}\right] \ell_{i}^{k}(x) \label{eq2} \tag{2}\]将 $\eqref{eq2}$ 式代入 $\eqref{eq1}$ 式,并要求 Maxwell 方程局部满足 DG 方法的强形式,从而得到半离散格式
\[\begin{aligned} \frac{d \boldsymbol{E}_{h}^{k}}{d t}+\frac{1}{J^{k} \varepsilon^{k}} \mathcal{D}_{r} \boldsymbol{H}_{h}^{k} &=\frac{1}{J^{k} \varepsilon^{k}} \mathcal{M}^{-1}\left[\ell^{k}(x)\left(H_{h}^{k}-H^{*}\right)\right]_{x_{l}^{k}}^{x_{r}^{k}} \\ &=\frac{1}{J^{k} \varepsilon^{k}} \mathcal{M}^{-1} \oint_{x_{l}^{k}}^{x_{r}^{k}} \hat{\boldsymbol{n}} \cdot\left(H_{h}^{k}-H^{*}\right) \ell^{k}(x) d x \end{aligned}\] \[\begin{aligned} \frac{d \boldsymbol{H}_{h}^{k}}{d t}+\frac{1}{J^{k} \mu^{k}} \mathcal{D}_{r} \boldsymbol{E}_{h}^{k} &=\frac{1}{J^{k} \mu^{k}} \mathcal{M}^{-1}\left[\ell^{k}(x)\left(E_{h}^{k}-E^{*}\right)\right]_{x_{l}^{k}}^{x_{r}^{k}} \\ &=\frac{1}{J^{k} \varepsilon^{k}} \mathcal{M}^{-1} \oint_{x_{l}^{k}}^{x_{r}^{k}} \hat{\boldsymbol{n}} \cdot\left(E_{h}^{k}-E^{*}\right) \ell^{k}(x) d x . \end{aligned}\]流量为
\[H^{*}=\frac{1}{\{\{Z\}\}}\left(\{\{Z H\}\}+\frac{1}{2} [\![ E ]\!] \right), \quad E^{*}=\frac{1}{\{\{Y\}\}}\left(\{\{Y E\}\}+\frac{1}{2} [\![ H ]\!]\right)\]其中
\[Z^{\pm}=\sqrt{\frac{\mu^{\pm}}{\varepsilon^{\pm}}}=\left(Y^{\pm}\right)^{-1}\]从而得到
\[\begin{aligned} H^{-}-H^{*} &=\frac{1}{2\{\{Z\}\}}\left(Z^{+} [\![ H ]\!] - [\![ E ]\!]\right) \\ E^{-}-E^{*} &=\frac{1}{2\{\{Y\}\}}\left(Y^{+} [\![ E ]\!]- [\![ H ]\!] \right) \end{aligned}\]作为进入半离散格式右端的惩罚项。
2. 数值实现
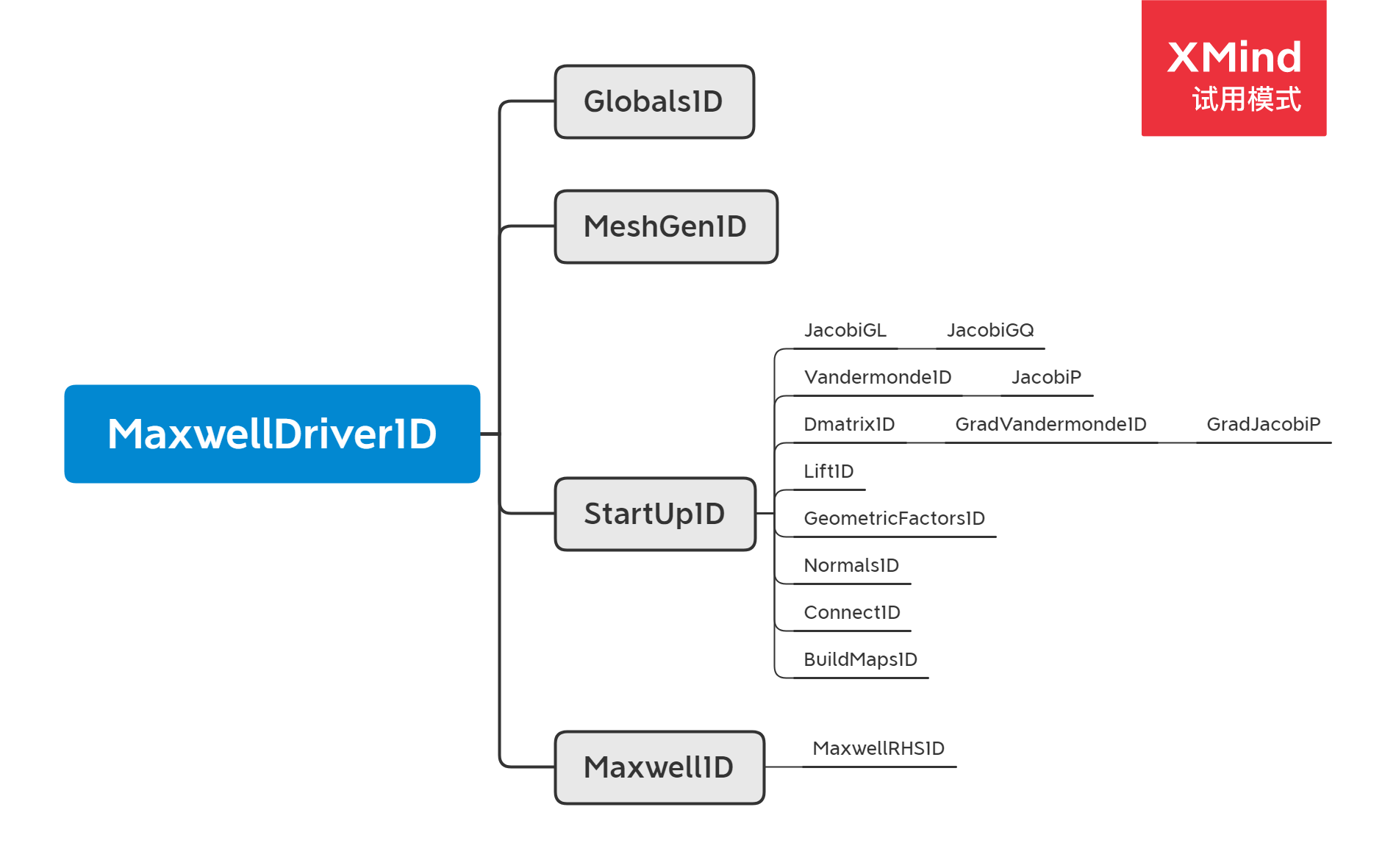
2.1 定义全局变量
Globals1D.m
% Purpose: declare global variables
global N Nfp Np K
global r x VX
global Dr LIFT
global nx Fx Fscale
global vmapM vmapP vmapB mapB Fmask
global vmapI vmapO mapI mapO
global rx J
global rk4a rk4b rk4c
global Nfaces EToE EToF
global V invV
global NODETOL
% Low storage Runge-Kutta coefficients
rk4a = [ 0.0 ...
-567301805773.0/1357537059087.0 ...
-2404267990393.0/2016746695238.0 ...
-3550918686646.0/2091501179385.0 ...
-1275806237668.0/842570457699.0];
rk4b = [ 1432997174477.0/9575080441755.0 ...
5161836677717.0/13612068292357.0 ...
1720146321549.0/2090206949498.0 ...
3134564353537.0/4481467310338.0 ...
2277821191437.0/14882151754819.0];
rk4c = [ 0.0 ...
1432997174477.0/9575080441755.0 ...
2526269341429.0/6820363962896.0 ...
2006345519317.0/3224310063776.0 ...
2802321613138.0/2924317926251.0];
2.2 生成网格节点
MeshGen1D.m
function [Nv, VX, K, EToV] = MeshGen1D(xmin,xmax,K)
% function [Nv, VX, K, EToV] = MeshGen1D(xmin,xmax,K)
% Purpose : Generate simple equidistant grid with K elements
% @ Nv: nunber of nodes K+1
% @ VX: row vector which covers K+1 vertex coordinates
% @ EToV: element to vertex, the number of the two vertices of the k-th unit
Nv = K+1;
% Generate node coordinates
VX = (1:Nv);
for i = 1:Nv
VX(i) = (xmax-xmin)*(i-1)/(Nv-1) + xmin;
end
% read element to node connectivity
EToV = zeros(K, 2);
for k = 1:K
EToV(k,1) = k; EToV(k,2) = k+1;
end
return
2.3 Legendre 多项式和节点单元
JacobiP.m
function [P] = JacobiP(x,alpha,beta,N);
% function [P] = JacobiP(x,alpha,beta,N)
% Purpose: Evaluate Jacobi Polynomial of type (alpha,beta) > -1
% (alpha+beta <> -1) at points x for order N and returns P[1:length(xp))]
% Note : They are normalized to be orthonormal.
% Note : alpha=beta=0, Legendre polynomial is a special case of Jacobian polynomial
% Turn points into row if needed.
xp = x; dims = size(xp);
if (dims(2)==1) xp = xp'; end;
PL = zeros(N+1,length(xp));
% Initial values P_0(x) and P_1(x)
gamma0 = 2^(alpha+beta+1)/(alpha+beta+1)*gamma(alpha+1)*...
gamma(beta+1)/gamma(alpha+beta+1);
PL(1,:) = 1.0/sqrt(gamma0);
if (N==0) P=PL'; return; end;
gamma1 = (alpha+1)*(beta+1)/(alpha+beta+3)*gamma0;
PL(2,:) = ((alpha+beta+2)*xp/2 + (alpha-beta)/2)/sqrt(gamma1);
if (N==1) P=PL(N+1,:)'; return; end;
% Repeat value in recurrence.
aold = 2/(2+alpha+beta)*sqrt((alpha+1)*(beta+1)/(alpha+beta+3));
% Forward recurrence using the symmetry of the recurrence.
for i=1:N-1
h1 = 2*i+alpha+beta;
anew = 2/(h1+2)*sqrt( (i+1)*(i+1+alpha+beta)*(i+1+alpha)*...
(i+1+beta)/(h1+1)/(h1+3));
bnew = - (alpha^2-beta^2)/h1/(h1+2);
PL(i+2,:) = 1/anew*( -aold*PL(i,:) + (xp-bnew).*PL(i+1,:));
aold =anew;
end;
P = PL(N+1,:)';
return
JacobiGQ.m
function [x,w] = JacobiGQ(alpha,beta,N);
% function [x,w] = JacobiGQ(alpha,beta,N)
% Purpose: Compute the N'th order Gauss quadrature points, x,
% and weights, w, associated with the Jacobi
% polynomial, of type (alpha,beta) > -1 ( <> -0.5).
if (N==0) x(1)= -(alpha-beta)/(alpha+beta+2); w(1) = 2; return; end;
% Form symmetric matrix from recurrence.
J = zeros(N+1);
h1 = 2*(0:N)+alpha+beta;
J = diag(-1/2*(alpha^2-beta^2)./(h1+2)./h1) + ...
diag(2./(h1(1:N)+2).*sqrt((1:N).*((1:N)+alpha+beta).*...
((1:N)+alpha).*((1:N)+beta)./(h1(1:N)+1)./(h1(1:N)+3)),1);
if (alpha+beta<10*eps) J(1,1)=0.0;end;
J = J + J';
%Compute quadrature by eigenvalue solve
[V,D] = eig(J); x = diag(D);
w = (V(1,:)').^2*2^(alpha+beta+1)/(alpha+beta+1)*gamma(alpha+1)*...
gamma(beta+1)/gamma(alpha+beta+1);
return;
JacobiGL.m
function [x] = JacobiGL(alpha,beta,N);
% function [x] = JacobiGL(alpha,beta,N)
% Purpose: Compute the N'th order Gauss Lobatto quadrature
% points, x, associated with the Jacobi polynomial,
% of type (alpha,beta) > -1 ( <> -0.5).
x = zeros(N+1,1);
if (N==1) x(1)=-1.0; x(2)=1.0; return; end;
[xint,w] = JacobiGQ(alpha+1,beta+1,N-2);
x = [-1, xint', 1]';
return;
Vandermonde1D.m
function [V1D] = Vandermonde1D(N,r)
% function [V1D] = Vandermonde1D(N,r)
% Purpose : Initialize the 1D Vandermonde Matrix, V_{ij} = phi_j(r_i);
V1D = zeros(length(r),N+1);
for j=1:N+1
V1D(:,j) = JacobiP(r(:), 0, 0, j-1);
end;
return
2.4 单元计算
GradJacobiP.m
function [dP] = GradJacobiP(r, alpha, beta, N);
% function [dP] = GradJacobiP(r, alpha, beta, N);
% Purpose: Evaluate the derivative of the Jacobi polynomial of type (alpha,beta)>-1,
% at points r for order N and returns dP[1:length(r))]
dP = zeros(length(r), 1);
if(N == 0)
dP(:,:) = 0.0;
else
dP = sqrt(N*(N+alpha+beta+1))*JacobiP(r(:),alpha+1,beta+1, N-1);
end;
return
GradVandermonde1D.m
function [DVr] = GradVandermonde1D(N,r)
% function [DVr] = GradVandermonde1D(N,r)
% Purpose : Initialize the gradient of the modal basis (i) at (r) at order N
DVr = zeros(length(r),(N+1));
% Initialize matrix
for i=0:N
[DVr(:,i+1)] = GradJacobiP(r(:),0,0,i);
end
return
Dmatrix1D.m
function [Dr] = Dmatrix1D(N,r,V)
% function [Dr] = Dmatrix1D(N,r,V)
% Purpose : Initialize the (r) differentiation matrices on the interval,
% evaluated at (r) at order N
Vr = GradVandermonde1D(N, r);
Dr = Vr/V;
return
2.5 网格构造及其运算
GeometricFactors1D.m
function [rx,J] = GeometricFactors1D(x,Dr)
% function [rx,J] = GeometricFactors1D(x,Dr)
% Purpose : Compute the metric elements for the local mappings of the 1D elements
xr = Dr*x; J = xr; rx = 1./J;
return
Normals1D.m
function [nx] = Normals1D
% function [nx] = Normals1D
% Purpose : Compute outward pointing normals at elements faces
Globals1D;
nx = zeros(Nfp*Nfaces, K);
% Define outward normals
nx(1, :) = -1.0; nx(2, :) = 1.0;
return
Connect1D.m
function [EToE, EToF] = Connect1D(EToV)
% function [EToE, EToF] = Connect1D(EToV)
% Purpose : Build global connectivity arrays for 1D grid based on standard
% EToV input array from grid generator
Nfaces = 2;
% Find number of elements and vertices
K = size(EToV,1); TotalFaces = Nfaces*K; Nv = K+1;
% List of local face to local vertex connections
vn = [1,2];
% Build global face to node sparse array
SpFToV = spalloc(TotalFaces, Nv, 2*TotalFaces);
sk = 1;
for k=1:K
for face=1:Nfaces
SpFToV( sk, EToV(k, vn(face))) = 1;
sk = sk+1;
end
end
% Build global face to global face sparse array
SpFToF = SpFToV*SpFToV' - speye(TotalFaces);
% Find complete face to face connections
[faces1, faces2] = find(SpFToF==1);
% Convert face global number to element and face numbers
element1 = floor( (faces1-1)/Nfaces ) + 1;
face1 = mod( (faces1-1), Nfaces ) + 1;
element2 = floor( (faces2-1)/Nfaces ) + 1;
face2 = mod( (faces2-1), Nfaces ) + 1;
% Rearrange into Nelements x Nfaces sized arrays
ind = sub2ind([K, Nfaces], element1, face1);
EToE = (1:K)'*ones(1,Nfaces);
EToF = ones(K,1)*(1:Nfaces);
EToE(ind) = element2; EToF(ind) = face2;
return
BuildMaps.m
function [vmapM, vmapP, vmapB, mapB] = BuildMaps1D
% function [vmapM, vmapP, vmapB, mapB] = BuildMaps1D
% Purpose: Connectivity and boundary tables for nodes given in the K # of elements,
% each with N+1 degrees of freedom.
Globals1D;
% number volume nodes consecutively
nodeids = reshape(1:K*Np, Np, K);
vmapM = zeros(Nfp, Nfaces, K); % u-
vmapP = zeros(Nfp, Nfaces, K); % u+
for k1=1:K
for f1=1:Nfaces
% find index of face nodes with respect to volume node ordering
vmapM(:,f1,k1) = nodeids(Fmask(:,f1), k1);
end
end
for k1=1:K
for f1=1:Nfaces
% find neighbor
k2 = EToE(k1,f1); f2 = EToF(k1,f1);
% find volume node numbers of left and right nodes
vidM = vmapM(:,f1,k1); vidP = vmapM(:,f2,k2);
x1 = x(vidM); x2 = x(vidP);
% Compute distance matrix
D = (x1 -x2 ).^2;
if (D<NODETOL) vmapP(:,f1,k1) = vidP; end;
end
end
vmapP = vmapP(:); vmapM = vmapM(:);
% Create list of boundary nodes
mapB = find(vmapP==vmapM); vmapB = vmapM(mapB);
% Create specific left (inflow) and right (outflow) maps
mapI = 1; mapO = K*Nfaces; vmapI = 1; vmapO = K*Np;
return
StartUp1D.m
% Purpose : Setup script, building operators, grid, metric and connectivity for 1D solver.
% Definition of constants
Globals1D; NODETOL = 1e-10;
Np = N+1; Nfp = 1; Nfaces=2;
% Compute basic Legendre Gauss Lobatto grid
r = JacobiGL(0,0,N);
% Build reference element matrices
V = Vandermonde1D(N, r); invV = inv(V);
Dr = Dmatrix1D(N, r, V);
% Create surface integral terms
LIFT = Lift1D();
% build coordinates of all the nodes
va = EToV(:,1)'; vb = EToV(:,2)';
x = ones(N+1,1)*VX(va) + 0.5*(r+1)*(VX(vb)-VX(va));
% calculate geometric factors
[rx,J] = GeometricFactors1D(x,Dr);
% Compute masks for edge nodes
fmask1 = find( abs(r+1) < NODETOL)';
fmask2 = find( abs(r-1) < NODETOL)';
Fmask = [fmask1;fmask2]';
Fx = x(Fmask(:), :);
% Build surface normals and inverse metric at surface
[nx] = Normals1D();
Fscale = 1./(J(Fmask,:));
% Build connectivity matrix
[EToE, EToF] = Connect1D(EToV);
% Build connectivity maps
[vmapM, vmapP, vmapB, mapB] = BuildMaps1D;
2.6 组合各部分
MaxwellRHS1D.m
function [rhsE, rhsH] = MaxwellRHS1D(E,H,eps,mu)
% function [rhsE, rhsH] = MaxwellRHS1D(E,H,eps,mu)
% Purpose : Evaluate RHS flux in 1D Maxwell
Globals1D;
% Compute impedance
Zimp = sqrt(mu./eps);
% Define field differences at faces
dE = zeros(Nfp*Nfaces,K); dE(:) = E(vmapM)-E(vmapP);
dH = zeros(Nfp*Nfaces,K); dH(:) = H(vmapM)-H(vmapP);
Zimpm = zeros(Nfp*Nfaces,K); Zimpm(:) = Zimp(vmapM);
Zimpp = zeros(Nfp*Nfaces,K); Zimpp(:) = Zimp(vmapP);
Yimpm = zeros(Nfp*Nfaces,K); Yimpm(:) = 1./Zimpm(:);
Yimpp = zeros(Nfp*Nfaces,K); Yimpp(:) = 1./Zimpp(:);
% Homogeneous boundary conditions, Ez=0
Ebc = -E(vmapB); dE (mapB) = E(vmapB) - Ebc;
Hbc = H(vmapB); dH (mapB) = H(vmapB) - Hbc;
% evaluate upwind fluxes
fluxE = 1./(Zimpm + Zimpp).*(nx.*Zimpp.*dH - dE);
fluxH = 1./(Yimpm + Yimpp).*(nx.*Yimpp.*dE - dH);
% compute right hand sides of the PDE's
rhsE = (-rx.*(Dr*H) + LIFT*(Fscale.*fluxE))./eps;
rhsH = (-rx.*(Dr*E) + LIFT*(Fscale.*fluxH))./mu;
return
Maxwell1D.m
function [E,H] = Maxwell1D(E,H,eps,mu,FinalTime);
% function [E,H] = Maxwell1D(E,H,eps,mu,FinalTime)
% Purpose : Integrate 1D Maxwell's until FinalTime starting with conditions (E(t=0),H(t=0))
% and materials (eps,mu).
Globals1D;
time = 0;
% Runge-Kutta residual storage
resE = zeros(Np,K); resH = zeros(Np,K);
% compute time step size
xmin = min(abs(x(1,:)-x(2,:)));
CFL=1.0; dt = CFL*xmin;
Nsteps = ceil(FinalTime/dt); dt = FinalTime/Nsteps;
% outer time step loop
for tstep=1:Nsteps
for INTRK = 1:5
[rhsE, rhsH] = MaxwellRHS1D(E,H,eps,mu);
resE = rk4a(INTRK)*resE + dt*rhsE;
resH = rk4a(INTRK)*resH + dt*rhsH;
E = E+rk4b(INTRK)*resE;
H = H+rk4b(INTRK)*resH;
end
% Increment time
time = time+dt;
end
return
MaxwellDriver1D.m
% Driver script for solving the 1D Maxwell's equations
Globals1D;
% Polynomial order used for approximation
N = 6;
% Generate simple mesh
[Nv, VX, K, EToV] = MeshGen1D(-1.0,1.0,80);
% Initialize solver and construct grid and metric
StartUp1D;
% Set up material parameters
eps1 = [ones(1,K/2), 2*ones(1,K/2)];
mu1 = ones(1,K);
epsilon = ones(Np,1)*eps1; mu = ones(Np,1)*mu1;
% Set initial conditions
E = sin(pi*x).*(x<0); H = zeros(Np,K);
% Solve Problem
FinalTime = 10;
[E,H] = Maxwell1D(E,H,epsilon,mu,FinalTime);
References
Hesthaven J S, Warburton T. Nodal discontinuous Galerkin methods: algorithms, analysis, and applications[M]. Springer Science & Business Media, 2007.
