img

suifeng

计算数学 / 机器学习

何晓峰

个人站

欢迎来到我的个人站~

Transfinite maps

| 阅读：次

Abstract

We present a method to generate a non-affine transfinite map from a given reference domain to a family of deformed domains. The map is a generalization of the Gordon–Hall transfinite interpolation approach. It is defined globally over the reference domain. Once we have computed some functions over the reference domain, the map can be generated by knowing the parametric expressions of the boundaries of the deformed domain. Being able to define a suitable map from a reference domain to a desired deformation is useful for the management of parameterized geometries.

Main idea

The idea behind the transfinite maps (TMs) is to deform the interior points of the physical domain through a linear combinations of the deformed points belonging to the boundaries.

Offline stage

For each side of the reference domain, we associate one weight function $\varphi_i$ with one projection function $\pi_ {i}$ .For a domain with $n$ sides, we have to solve $2n$ elliptic problems; however, these computations are independent of the deformation (and so of the parameter $\mu$ ) and they could be included in the offline stage (computed just once) to guarantee computational efficiency.

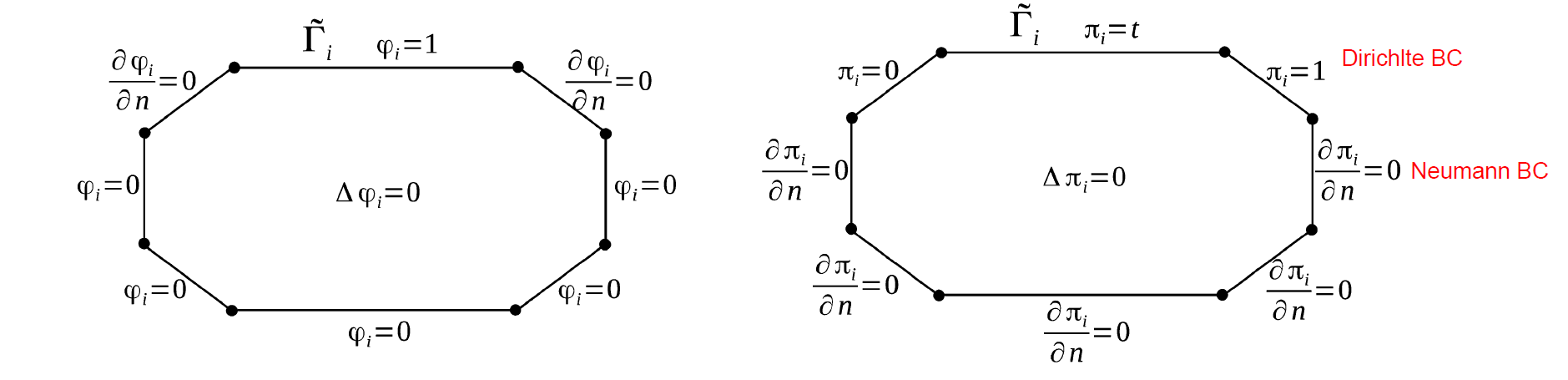
\[\left\{\begin{array}{ll} \Delta \varphi_ {i}=0 & \text { in } \tilde{\Omega}, \\ \varphi_ {i}=1 & \text { on } \tilde{\Gamma}_ {i}, \\ \frac{\partial \varphi_ {i}}{\partial n}=0 & \text { on } \tilde{\Gamma}_ {j}, j=i-1, i+1, \\ \varphi_ {i}=0 & \text { on } \tilde{\Gamma}_ {j}, j \neq i-1, i, i+1 \end{array}\right.\] \[\left\{\begin{array}{ll} \Delta \pi_ {i}=0 & \text { in } \tilde{\Omega} \\ \pi_ {i}=t & \text { on } \tilde{\Gamma}_ {i} \\ \pi_ {i}=0 & \text { on } \tilde{\Gamma}_ {i-1}, \\ \pi_ {i}=1 & \text { on } \tilde{\Gamma}_ {i+1}, \\ \frac{\partial \pi_ {i}}{\partial n}=0 & \text { on } \tilde{\Gamma}_ {j}, j \neq i-1, i, i+1, \end{array}\right.\]

Online stage

Let $\Omega=\Omega(\boldsymbol{\mu})$ be a parameterized domain. We suppose that $\Omega$ is a curved polygonal with the same number $n$ of edges. Let each edge $\Gamma_ {i}, i=1, \ldots, n$ be parameterized trough the parameter $\mu \in \mathcal{D}$ by a bijective map $\psi_ {i}:[0,1] \times \mathcal{D} \rightarrow \Gamma_ {i}$ such that $\boldsymbol{\psi}_ {i}(1, \boldsymbol{\mu})=\boldsymbol{x}_ {i}$, where $\boldsymbol{x}_ {i}$ denotes the vertex shared by $\Gamma_ {i}$ and $\Gamma_ {i+1}$, and $\boldsymbol{\psi}_ {i}(0, \boldsymbol{\mu})=\boldsymbol{x}_ {i-1}$, where $\boldsymbol{x}_ {i-1}$ denotes the vertex shared by $\Gamma_ {i}$ and $\Gamma_ {i-1}$. We denote by $\tilde{\boldsymbol{x}}$ a generic point of the reference domain $\tilde{\Omega}$ and by $\boldsymbol{x}$ a generic point of the parameterized domain $\Omega$. The transfinite map proposed is defined as:

\[\boldsymbol{T}(\tilde{\boldsymbol{x}}, \boldsymbol{\mu})=\sum_ {i=1}^{N}[\phi_ {i}(\tilde{\boldsymbol{x}}) \boldsymbol{\psi}_ {i}(\pi_ {i}(\tilde{\boldsymbol{x}}), \boldsymbol{\mu})-\phi_ {i}(\tilde{\boldsymbol{x}}) \phi_ {i+1}(\tilde{\boldsymbol{x}}) \boldsymbol{x}_ {i}].\]

The advantage of such a map is that for each parameterized domain $\Omega(\boldsymbol{\mu})$, we need only to compute the boundary expressions $\boldsymbol{\psi}_ {i}\left(\pi_ {i}(\tilde{\boldsymbol{x}}), \boldsymbol{\mu}\right)$ and to perform the linear combination.

Boundary displacement-dependent transfinite maps

Main idea

The basic idea of the Boundary Displacement-Dependent Transfinite Map $(B D D T M$ is to keep into account the original positions of the points in the reference domain $\tilde{\Omega}$ and to move them by weighting only the difference between the original boundaries and the deformed ones.

Let $\mathcal{D}$ be the parameter domain, we define the displacement function $ \boldsymbol{d}_ {i} : [0,1] \times \mathcal{D} \rightarrow \Gamma_ {i}$ as:

\[\boldsymbol{d}_ {i}(t, \boldsymbol{\mu})=\boldsymbol{\psi}_ {i}(t, \boldsymbol{\mu}) - \tilde{\boldsymbol{\psi}}_ {i}(t)\]

If $\tilde{x}$ is a generic point in the reference domain $\tilde{\Omega}$, The idea of the BDD TM is to displace it through the quantity $\tilde{\boldsymbol{x}}+\sum_ {i=1}^{N} \phi_ {i}(\tilde{\boldsymbol{x}}) \boldsymbol{d}_ {i}\left(\pi_ {i}(\tilde{\boldsymbol{x}}), \boldsymbol{\mu}\right) .$ As in the previous map, in every term we have to subtract a correction term, which is, in this case, $\phi_ {i}(\tilde{\boldsymbol{x}}) \phi_ {i+1}(\tilde{\boldsymbol{x}}) \boldsymbol{d}_ {i}(1, \boldsymbol{\mu})$, such that the BDD Transfinite Map is defined as:

\[\boldsymbol{S}(\tilde{\boldsymbol{x}}, \boldsymbol{\mu}) = \tilde{\boldsymbol{x}}+\sum_ {i=1}^ {N} \left[\phi_ {i}(\tilde{\boldsymbol{x}}) \boldsymbol{d}_ {i}\left(\pi_ {i}(\tilde{\boldsymbol{x}}), \boldsymbol{\mu}\right)-\phi_ {i}(\tilde{\boldsymbol{x}}) \phi_ {i+1}(\tilde{\boldsymbol{x}}) \boldsymbol{d}_ {i}(1, \boldsymbol{\mu})\right]\]

Conclusion

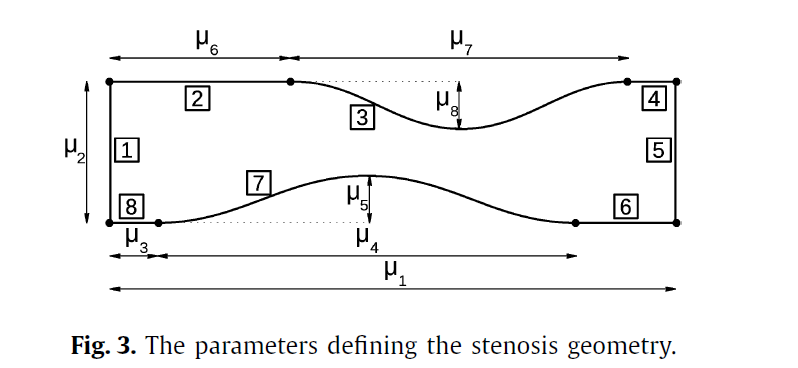
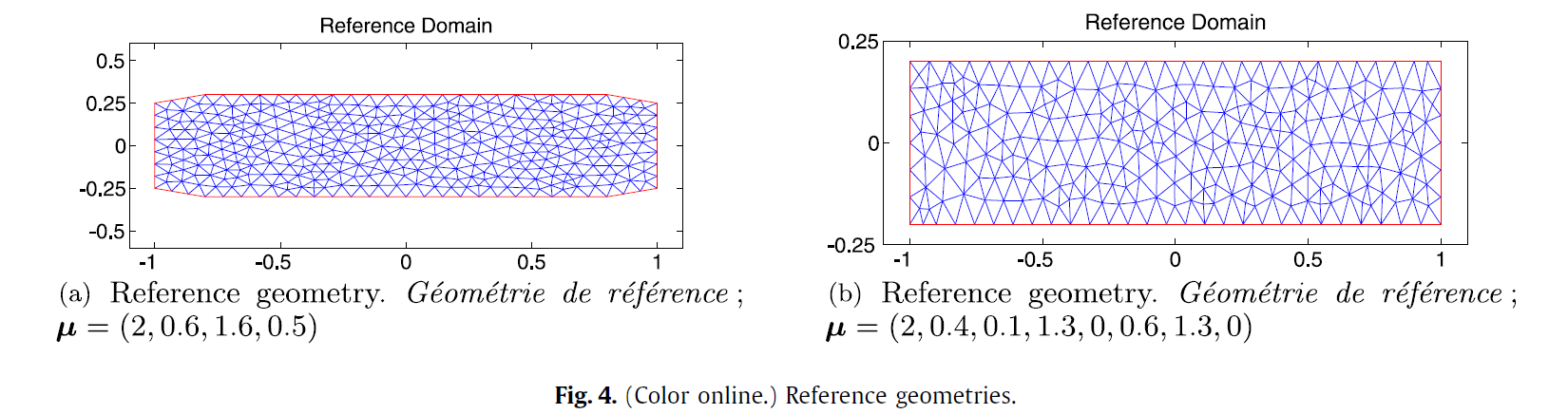
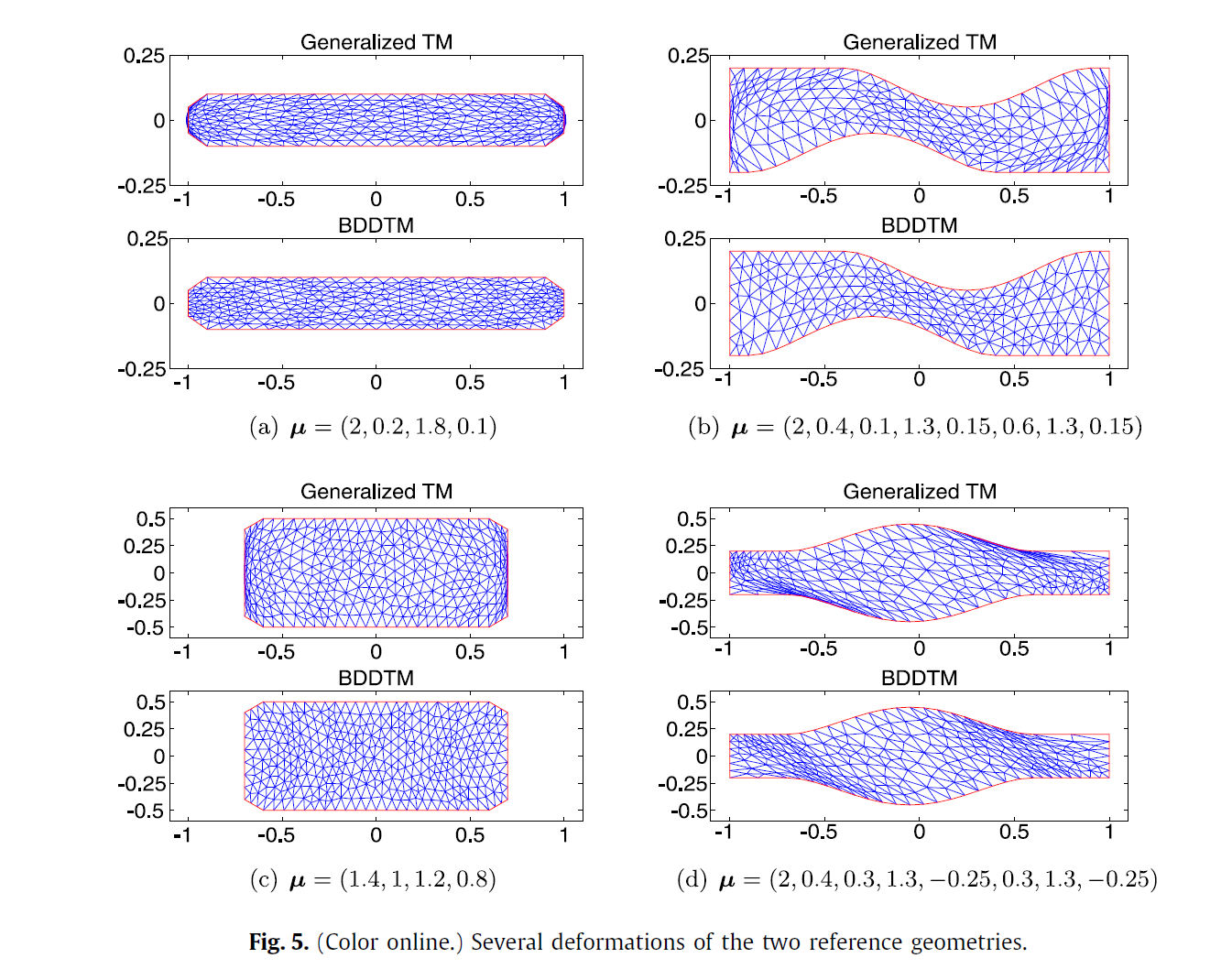
We can observe that in both cases the meshes deformed by the BDD TM are much more regular and there is no overlapping between the triangles of the mesh. In particular, with the BDD TM, the position of the domain in the Cartesian coordinate plane does not affect the effectiveness of the map. Moreover, the new proposed map allows us to deal with more complex parameterizations of the domain and consequently bigger deformations of the geometry without producing any overlapping phenomena between the triangles of a mesh defined in the domain.